Quelle place tiennent les Mathématiques dans la période de la Renaissance ?

Conclusion :

        Pour conclure, nous pouvons dire que les mathématiques ont une place assez importante pendant la Renaissance mais que les plus grandes découvertes se font dans la période suivante, le Classicisme, et que les humanistes s'intéressent beaucoup plus à la littérature et à la philosophie. Les mathématiques ont tout de même servi aux artistes et aux scientifiques, tel que les physiciens, les astronomes, les architectes ...etc. Ils ne sont pas enseignés en priorités dans les écoles, cependant il en sort beaucoup de savants tel que Fibonacci, Viète, Tartaglia, Cardan ou bien Kepler.

Les mathématiques ne sont que rarement utilisés seuls , à cette époque, ils contribuent à la recherche dans les domaines scientifiques et artistiques. La littérature est bien plus importante.

De nos jours, les mathématiques et la littérature ont une place de la même importance.

B- Exemple de gravure.

Les Ambassadeurs ( 1533 ) d'Hans Holbein le jeune.

L'étude de cette gravure célèbre nous permet de montrer quels sont les instruments mathématiques de l'époque de la Renaissance et quelles sont les caractéristiques d'une peinture de cette époque.

Les Ambassadeurs est un portrait de Jean de Dinteville et Georges de Selve. C'est un chef-d'œuvre

par sa richesse symbolique et par l'étonnant réalisme de la peinture.

Le tableau comporte un étrange objet au premier plan resté longtemps mystérieux. C'est en faite un crâne humain déformé qui fait référence à la vanité de tous les symboles présents dans le tableau. Les principaux symboles sont les objets mathématiques qui se rattache au quadrivium : l'arithmétique, la géométrie, la musique et l'astronomie. On distingue en effet un globe terrestre, deux livres, un luth et quatre flutes, sur l'étagère du haut une sphère céleste, des objets de mesure du temps, un autre livre, le tout posé sur un tapis rouge aux motifs géométriques complexes. A l'arrière plan, nous voyons un rideau de velours vert. Celui-ci dispose d'un repli qui révèle, dans le coin à gauche, un crucifix. Le sol est un pavage composé de cercles et de carrés où se détache une forme appelé l'os de seiche.

Jean de Dinteville ( personnage de gauche ) est richement habillé d'un manteau de fourrure, il porte à la main une dague dans un étui, un béret sur la tête. Du noir de ses vêtements tranche le rouge de ses manches et de sa poitrine où pend à une chaîne dorée, une médaille décorée d'un ange.

Georges de Selve est, lui, tout vêtu de noir, enveloppé dans un manteau de fourrure. Il porte une paire de gants dans la main droite et sa tête porte une coiffe.

Ainsi, ce premier regard jeté sur la peinture, une œuvre quasiment carrée, de plus de deux mètres de côté, amène deux réflexions distinctes. Tout d'abord, les deux sujets du tableau n'en occupent pas le centre mais sont déportés à droite et à gauche, encadrant un ensemble d'objets qui semblent, au premier abord, hétéroclites (= de styles différents.).

Puis, à leurs pieds, se trouve un objet énigmatique. Celui-ci est comme étranger au reste du tableau bien qu'il en occupe le premier plan. On peut supposer qu'Holbein à préférer mettre en valeur autre chose que les personnages qui pourtant donnent leur nom à l'œuvre.

III- Représentation des mathématiques :

Les mathématiques sont diffusés à travers des livres de savants tels que Rabelais, Montaigne, Érasme, mais aussi grâce aux œuvres de grands artistes comme Léonard De Vinci, Albrecht Dürer.

En effet, cette préoccupation pour le quantitatif, le mathématique de la part des marchands touche aussi un groupe auquel on a l'habitude une place centrale dans l'analyse de la Renaissance, celui des artistes.

A-L'artiste et son apogée.

Florentin Leon-Battista Alberti ( 1404-1472 ) dans son De pitura de 1435 trace le programme d'un vie d'artiste selon les principes de l'humanisme. Selon lui, un peintre accompli serait « avant tout un homme de bien instruit dans las arts libéraux » et il devrait « très bien posséder la géométrie ». La première partie de l'œuvre est justement consacrée à la perspective géométrique, reposée sur les travaux d'Euclide. L'artiste doit connaître les proportions et les séparations des surfaces.

Pour Alberti, le modèle de l'artiste était Filippo Brunelleschi ( 1377-1446 ) : il est le premier à avoir posé ses bases théoriques sur les Éléments d'Euclide.

Mais le plus grands artiste de l'époque est évidemment Léonard De Vinci ( 1452-1519 ). Nous pouvons rappeler que l'ouverture de l' « âge moderne » dans les arts se fait grâce aux progrès de la perspective notamment ceux qu'a effectué De Vinci vers 1500. Comme la plupart des artistes, il étudie à l'école d'abaque puis devient apprenti à Florence dans l'atelier d'un artiste accompli. Après cela, il se mit au service d'un prince une fois il fut célèbre. Ce prince a un rôle de mécène: il aide financièrement des artistes pour se former une certaine réputation et bénéficier de leurs ingéniosités. Les artistes suivent les vœux de leur maître et peuvent ainsi être reconnu et exercer leur art sous la protection d'hommes puissants et riches. Les premiers mécènes étaient les Médicis, la famille du duc de Florence, en Italie au XVe siècle. C'est d'ailleurs à partir de cette période et de cette famille qu'on détermine le commencement de l'époque de la Renaissance.

« L'Homme de Vitruve » de Léonard de Vinci

Le deuxième nom que l'on peut retenir est Albrecht Dürer ( 1471-1528 ). Il est mathématicien, graveur et peintre. Il s'instruit dans les Éléments d'Euclide, puis dans De architectura de Vitruve, et dans les travaux d'Alberti et Pacioli. L'œuvre qui illustre le mieux son goût pour les mathématiques est « Mélancholia ».

En effet, il trace dans sa gravure un carré magique ( zoom ci-dessous ), dont les verticales, horizontales et les diagonales ont pour somme 34, et il arrive même à faire figurer la date de l'œuvre dans la dernière ligne: 1514. Il fait apparaître aussi un polyèdre, et a le souci des proportions (celles du cheval et de l'homme).

On peut trouver de nombreuses gravures de la période de la Renaissance représentant les instruments mathématiques et l'Arithmétique.

Le plus célèbre tableaux où figurent des instruments propres aux mathématiciens est Les mesureurs. Son auteur n'est pas connu précisément, mais on peut voir qu'il veut nous montrer l'usage des mathématiques dans des activités pratiques telles que la couture, (la cuisine), le dessin, le commerce... que chaque personnage effectue. On voit au premier plan des compas, un rapporteur, des équerres, une règle dans les mains de la dame sur la droite, une balance au fond à gauche...

C- Les métiers autour des Mathématiques.

Les Mathématiques ouvrent plusieurs portes professionnelles telles que sur le métier d'ingénieur-architecte. Ce métier prit essor en Italie au XV° siècle, plus précisément à Florence, une ville du nord de l'Italie.

C'est Filippo Brunelleschi ( 1377-1446) le premier à avoir posé des bases théoriques sur « Les éléments » d'Euclide qui a construit la cathédrale de Santa Maria dei Fiori.

Il est ingénieur-architecte, ingénieur militaire et peintre. On peut donc le considérer comme un artiste.

Léonard De Vinci ( 1452-1519) est à la fois artiste, scientifique, ingénieur, inventeur, anatomiste, peintre, sculpteur, architecte, urbaniste, botaniste, musicien, poète, philosophe et écrivain. C'est vers 1500 que l'on parle de l'ouverture de l' « âge moderne » dans les arts grâce à lui. En effet avec la perspective on commence à construire plus aisément des machines.

Tartaglia (1499-1557) écrivait en 1546: « Celui qui désire contempler de nouvelles inventions qu'il ne les cherche pas dans Platon ou Plotin [ surnom donné au savant Platon] ou de quelqu'autre ancien grec ou romain, mais seulement du métier, de la mesure et de la théorie » . Cela ne veut pas dire qu'il s'oppose aux inventions antiques mais qu'il veut créer des édifices propre à son temps.

Les astronomes ont eux aussi suivis des études mathématiques,on parle d'ailleurs de Révolution astronomique ou copernicienne durant la période de la Renaissance qui aura des conséquences à long termes.

Tycho Brahé ( 1546-1601 ) astronome danois fut un adversaire du système de Copernic que l'on exposera plus tard. Il fut le premier a tenir compte de la réfraction de la lumière et rédigea un catalogue de 777 étoiles, il inventa un système planétaire qui va dans le sens de celui de Ptolémée :

« Le système de Tycho Brahé: Le Soleil et la Lune tourne autour de la Terre qui est immobile au centre de l'univers; les autres planètes tournent autour du Soleil. »

Nicolas Copernic, représentant typique de l'Humanisme néoplatonicien ( il s'inspire de Platon) est un grand astronome Polonais ( 1473-1543 ). Il trouve le système de Ptolémée insuffisant, ce qui le mène à élaborer une nouvelle théorie des mouvements planétaires en passant du géocentrisme ( mouvements des planètes autour de la Terre ) à l'héliocentrisme ( double mouvement des planètes sur elles-même et autour du Soleil ).

N.B: Cette théorie fut à l'origine de la Révolution scientifique du XVII° siècle, car elle fut publiée après sa mort.

Johan Kepler ( 1571-1630 ) est le successeur de Tycho Brahé. Il inventa un nouveau modèle géométrique du système solaire:

Ce modèle est constitué de solides inscrits les uns dans les autres. Les sphères représentent les planètes en prenant la Terre comme unité.

Nicolas Copernic ( 1473-1543 ) est l'auteur d'une théorie selon laquelle le soleil est le centre de l'univers et la terre tourne autour de lui. Ce qui l'oppose donc à un grand nombre d'astronomes de son temps dont Tycho Brahé. On parle de révolution copernicienne, elle fut publiée et contestée après sa mort.

Système de Copernic.

Galilée ( 1564-1642 ) est un physicien et astronome italien qui défend ardemment les idées de Copernic. Il perfectionne la lunette astronomique et dans le domaine des mathématiques et de la physique il fait avancer les connaissances sur la cinématique (= discipline qui étudie le mouvement des corps) et de la dynamique (= discipline qui étudie les forces appliquées aux corps)

Au XVI° siècle, non seulement il n'y a pas d'opposition entre les humanités et la science, mais au contraire celles-là étaient mobilisées pour les besoins de celle-ci. Tout comme les mathématiques étaient mobilisées pour les besoins de l'ingénierie, de l'architecture, de la physique, de l'astronomie et enfin de l'art.

B- Le cursus.

Pour apprendre les mathématiques durant la période de la Renaissance il faut suivre un certain cursus.

Ce dernier commence au collège, qui comprend l'enseignement primaire et secondaire, et pour réformer l'homme nouveau les humanistes décident de les réformer. Un des plus grands collège de France est celui de Paris: le Collège des Lecteurs Royaux.

Les universités étaient, à l'époque, des associations d'étudiants ou de maîtres et d'étudiants, elles étaient indépendantes de l'Église contrairement à celles du Moyen-Age. L'une des premières universités d'Europe fut construite au milieu du XII siècle. Depuis de nombreuses universités furent fondées à travers l'Europe. Mais au cours de temps leurs membres se font reconnaître au Clergé sans avoir à faire partie de l'Église. C'est au cours des XIII°, XIV° et XV° siècles que le nombre d'université augmente rapidement. C'est ainsi qu'on voit apparaître l'université de Paris, de Oxford et de Montpellier où l'enseignement était divisé en plusieurs facultés dont la faculté des arts qui enseignait le Trivium et le Quadrivium. Ces matières comprennent la musique, l'arithmétique, la géométrie et l'astronomie. Ici encore on constate que les mathématiques ont une place limitée dans l'éducation humaniste. Les étudiants commençaient leurs études universitaires, après le collège vers l'âge de quatorze ans en s'inscrivant au baccalauréat de la faculté des arts mais très peu d'entre eux y demeuraient plus de deux ans.

Étrangement, dans certaines universités les étudiants les plus doués, spécialisés dans l'enseignement des sciences et de la philosophie en compétition les uns avec les autres pour l'obtention de postes, payaient directement les maîtres pour leurs cours.

«  Les universités européennes selon leur période de fondation »

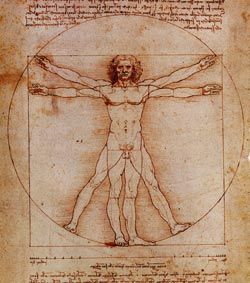
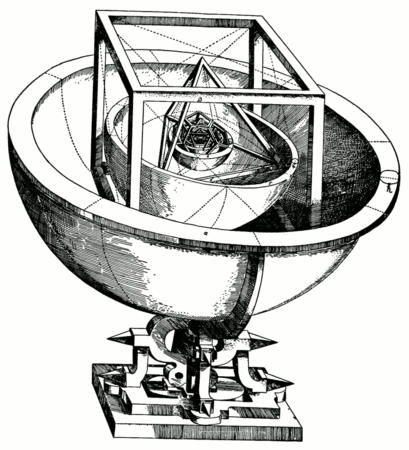
B- Évolution dans la période de la renaissance :

Ce qui intéressait le plus les intellectuels médiévaux dans les mathématiques, c'était le côté logique. Ainsi, les discussions portaient moins sur le contenu des théorèmes géométriques que sur leur forme et les rapports qui les unissaient.

a- Culture mathématique :

La culture urbaine italienne accordait une grande importance au nombre, au quantitatif, à l'aspect pratique des choses. Il s'agissait ici d'abord de l'arithmétique, essentielle aux échanges des marchands, mais aussi de la mesure des distances, qui fait appel à la géométrie et celle des volumes et des poids, pour l'estimation des coûts.

L'arithmétique commerciale fut donc très importante pour les pratiques marchandes.

Le livre de l'abaque de Fibonacci ( 1180-1250 ), aussi connu sous le nom de Léonard de Pise visait à remplacer l'usage des chiffres romains, qui se prêtent mal au calcul, par les chiffres arabes et il présentait aussi certaines applications de l'arithmétique au commerce.

Le calcul avec les chiffres arabes devait finir par rendre caduc l'usage de l'abaque ; il allait aussi favoriser l'apparition dans les villes italiennes au début du XIV° siècle, de l'outil clé pour le commerce, c'est à dire de la comptabilité à double entrée.

Luca Pacioli ( 1445- 1514 : un mathématicien franciscain à qui Léonard de Vinci demandera des cours de maths à la fin des années 1490 ) , publia à Venise en 1494 la grande synthèse de l'arithmétique commercial, la Summa de arithmetica, geometria, proportioni et proportionalita.

Il fut traduit en plusieurs langues, dont le latin.

On parle de diffusion d'une mentalité numérique, notamment grâce aux œuvres citées.

La multiplication des instituts bancaires et des outils de crédits, la naissance des assurances, le droit de comptabilité d'entreprise, mais aussi les pratiques du recensement et de taxation des cités-Etats imposaient en effet une connaissance de plus en plus générale de l'univers des nombres.

b- Interview de Yves André, Directeur de recherches en mathématiques au CNRS de Paris :

Question de Alice, Audrey et Émeline: Léonard De Vinci a-t-il apporté quelque chose aux Mathématiques?

Y. André: Léonard De Vinci n'a pas de contribution directe aux Mathématiques.

Il a étudié les solides platoniciens, Archimède... mais il se sert de cet apprentissage surtout pour le mettre en image. Il a malgré tout découvert et étudier le phénomène de la turbulence.

Il travailla avec Luca Pacioli durant des voyages qu'ils parcoururent ensemble, et il illustra ses oeuvres: une Encyclopédie où Pacioli parle de la théorie des proportions, et De divina porportione ce qui signifie « de la divine proportion » où il parle du nombre d'Or qui régit les proportions des tableaux de la Renaissance.

Spirale du nombre d'Or.

Le rectangle d'Or est un rectangle formé d'un carré et d'un rectangle qui lui est proportionnel. Lorsque le carré à pour côté 1, le rectangle a pour longueur le nombre d'Or: (1+ 5 )/2 .

La spirale obtenue est une spirale équiangulaire qui se rencontre beaucoup dans la nature : coquilles d'escargots, nombres de pétales de marguerites ou d'autres fleurs.

« La flagellation du Christ », un tableau de De La Francesca est, par exemple dans les proportions divines donc régi par ce nombre d'Or. On peut en effet le couper en deux parties, séparée par une colonne: un carré, à gauche, et un rectangle qui lui est proportionnel, à droite. De La Francesca a écrit un livre en latin qui explique la géométrie du tableau. Celui-ci fut traduit puis inclut, sans faire référence à son véritable auteur, dans une oeuvre de Pacioli.

On retrouve le nombre d'Or chez Fibonacci, dans sa suite de nombres appelée « suite de Fibonacci ». Un nombre de la suite s'obtient en ajoutant les deux nombres précédents de la suite.

On a ainsi:

1 1 2 3 5 8 13 21 34 55 89 etc...

Lorsqu'on calcule les quotients: 2/1 3/2 5/3 8/5 etc... on remarque qu'on obtient des nombres de plus en plus proches les uns des autres ( sans jamais être égaux ) et qui se rapprochent du nombre d'Or.

Il figure sur une peinture mystérieuse qui pose beaucoup de questions:

• De qui est ce tableau?

• Que fait-il avec sa main droite?

• Qui est l'élève qui se tient derrière lui?

On sait par contre que le solide représenté en haut à gauche est un polyèdre probablement fait par Léonard De Vinci car ingénieux: il est en perspective très réaliste et on peut voir l'eau qu'il contient se refléter sur toutes ses faces.

Luca Pacioli a demandé que l'on mette une spirale d'or sur sa tombe, mais on a en fait dessiné une spirale euclidienne:

Il doit être terriblement déçu!

I- La conception des Mathématiques.

L'histoire des Mathématiques s'étend sur plusieurs millénaires et dans de nombreuses régions du globe, allant de la Chine à l'Amérique centrale. Le développement des connaissances mathématiques s'effectue essentiellement de façon indépendante partout sur Terre.

A- Son origine antique et ses inventions.

Tous les mathématiciens de la Renaissance s'appuient sur les recherches et inventions d'origine antique. C'est pourquoi nous allons nous pencher en premier sur les grands scientifiques de l'Antiquité :

- Thalès (-624;-548) , célèbre mathématiciens pour la découverte du théorème portant son nom. Selon lui, dans un triangle ABC : AB'/AB=AC'/AC=B'C'/BC avec B' un point de [AB] et C' un point de [AC] tels que (B'C') soit parallèle à (BC).

- Pythagore (-569;-475) invente un théorème qui porte son nom où il démontre que « Si un triangle est rectangle, alors le carré de l'hypoténuse est égal à la somme des carrés des deux côtés du triangle. ». Ce qui s'écrit: AB² =AC² +BC² pour un triangle ABC rectangle en C.

- Euclide ( IV° siècle avt J-C ) , grand mathématicien et philosophe grec, est connu pour son œuvre phénoménal les Éléments qui servira de base à toute la géométrie pendant plus de deux milles ans. Une vraie encyclopédie, composée de treize livres, qui traite des figures géométriques, des polygones inscrits et circonscrits à un cercle, des proportions, de la géométrie dans l'espace ainsi que des nombres. Il démontre et défini des théorèmes de ces ancêtres, comme ceux de Thalès et de Pythagore, et deux livres seront complétés plus tard par Archimède; on parle de géométrie euclidienne. Il invente aussi un algorithme portant son nom permettant de calculer le PGCD ( Plus Grand Dénominateur Commun ) d'un nombre.

-Diophante un mathématicien grec du III° siècle avt J-C. Son œuvre la plus célèbre consacrée à la résolution de problèmes s'appelle les Arithmétiques. Il est surnommé le «  père de l'algèbre » par les mathématiciens du XVI° et du XVII° siècle. Il a donné son nom aux équations diophantiennes; ce sont des équations à plusieurs inconnues et à coefficients entiers ou rationnels qui mènent à un grand nombre de solutions entières ou rationnelles.

Introduction

En rapport avec le couple mathématiques-littérature, nous avons choisi d'étudier le thème «  Savants et Sciences : Hier et aujourd'hui » . Nous nous sommes intéressées aux mathématiques de la Renaissance vu par les humanistes.

Tout d'abord il faut savoir que le Renaissance constitue une période fondatrice d'une ère nouvelle, marquée par un retour aux idéaux de la culture grecque et romaine, et au cours de laquelle de nouvelles formes de gouvernements, d'arts et de savoir apparurent. Le Renaissance reprend des idées de l'Antiquité. Elle commence en Italie au XV° siècle à Florence grâce aux Médicis, qui furent les premiers mécènes ( maîtres des artistes ).

Nous avons décidé de nous pencher sur la conception des mathématiques de cette époque en énumérant les grandes dates puis en approfondissant les connaissances qu'ils ont dans cette matière. Puis sur l'enseignement des mathématiques que les humanistes donnent à leurs élèves . Ainsi nous allons parler de la méthode scolastique et de l'apologie du savoir, deux caractéristiques de l'éducation humaniste, du cursus qu'il faut emprunter pour devenir un véritable savant en mathématiques, et des métiers sur lesquels débouche ce cursus. Enfin, nous analyserons la représentation des mathématiques à travers des peintures et leurs œuvres.  

Sommaire

Introduction.

I- La conception des mathématiques.

A- Les grandes dates.

a- Les origines antiques.

b- Les grandes découvertes de la Renaissance.

B- Évolution dans la période de la Renaissance.

a- Cultures mathématiques de la Renaissance.

b- Interview de Yves André, directeur de recherches en mathématiques au CNRS de Paris.

II- L'enseignement des mathématiques durant la période de la Renaissance.

A- La méthode scolastique et l'apologie du savoir.

B- Le cursus.

C- Les métiers autour de mathématiques.

III- Représentation des mathématiques.

A- L'artiste et son apogée.

B- Exemple de gravure.

Conclusion.